Chapter 3 Spatial data in R
3.1 Overall goal of the chapter
The previous chapter presented concisely the focus of this book and what the reader would be able to achieve after reading it. This chapter will focus on the fundamentals of mapping, i.e. the different types of data that can be used to make a map.
It is written for those with some knowledge of R and little experience with spatial data. If you are familiar with the different data types (points, lines, polygons and vectors), you may move on to the next chapter where visualisation of data types is explained in more detail. However you never know, you may learn something here too.
Learning objectives
- Be able to describe and use points, lines, polygons and raster data types
- Understand the difference between vector and raster data
- Know how to manipulate spatial data using packages
sffor vector andrasterfor raster. [andy: consider whether to replacerasterwithterraorstarsabove] - Be comfortable visualising different spatial data types in R using packages
mapview&tmap
Maps are used for a wide range of purposes. In this book we focus on using maps to present data.
A map can provide a model of reality to help the reader see where things or events are located. This could be on the scale of a street, a neighbourhood, a country or a continent. Depending on the topics you’re interested in, this could be focussed on disease cases, landcover dynamics, location of schools. The opportunities are endless.
The data that we can represent on a map can be divided into four main types :
- points
- lines
- polygons
- rasters
Points can be used to represent the locations of e.g. cities, buildings, disease cases, sample sites or wildlife records. They can be used to represent the centre of an area. Points can be chosen when the shape of the location is not important. Thus for a map representing a continent, cities can be represented by points because the area of cities would not be visible. Lines may represent physical features such as rivers or roads, or routes travelled, or abstract links between point locations. Polygons are shapes that can represent the boundaries of countries, regions or cities or if you are zoomed in further the outline of buildings. Rasters are gridded datasets that can be used to represent anything that covers a continuous area, this could be temperature or estimates of population or landcover, most often they are derived from remote sensing and modelling.
[andy work a bit more on previous paragraph]
All spatial data types require a coordinate reference system (CRS) identification to place data in the correct location on the Earth. We will discuss this in more detail later. For now, just be aware that a code may need to be entered to ensure that data display in the correct place. Note also that spatial data types can be stored in many different formats, from Shapefile (.shp + .dbf + .prj + …), to GeoPackage (.gpkg), to CSV files (.csv). To learn more about the possible spatial data types go to Chapter 4: Getting your own data into R.
3.2 Points
Let’s take an imaginary walk outside. What do you see? Houses, cars, trees… All these objects have unique coordinates that can be used to identify their location. On a map, the objects can be drawn as points with their latitude and longitude coordinate indicating their location in relation to other objects and places. Depending on the scale of your map, points can represent anything from a house, health clinic, city or district. You, as the map creator, can decide the scale of your own map.
3.2.1 Example
Lets try and visualise the capital cities of Africa which we have stored in the afrilearndata package.
Just a quick reminder of the necessary packages
library(afrilearndata) #load afrilearndata package
#In case the data isn't loaded into your R environment automatically, it can be loaded individually using the code below.
data(africapitals) #location of the African capitalsWe will start by downloading the necessary packages: sf package. This package is necessary to read in the spatial data files. tmap package. This package is necessary to create the maps.
#install.packages("sf") #install sf package
#install.packages("tmap") #install tmap package
library(sf) #load sf package
library(tmap) #load tmap packageNote More information can be found about the different packages using the Help tools.
Now, let’s look at the data file that contains information about the African capitals. A quick summary of the spatial aspects (geometry) of the datafile can be checked using the following code:
print(st_geometry(africapitals)) #printing information on the geometry## Geometry set for 51 features
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -17.48 ymin: -29.31 xmax: 47.51 ymax: 36.84
## Geodetic CRS: WGS 84
## First 5 geometries:We can see from the results that the African capital data file contains 50 points (capitals) with geometry type POINT.
Let’s print the first 6 rows of data, so we can see how the coordinates of each African capital is stored in the database.
head(africapitals) #First 6 rows of data are printed## Simple feature collection with 6 features and 4 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: -0.2 ymin: -18.89 xmax: 47.51 ymax: 36.77
## Geodetic CRS: WGS 84
## capitalname countryname pop iso3c geometry
## 280 Abuja Nigeria 178462 NGA POINT (7.17 9.18)
## 308 Accra Ghana 2029143 GHA POINT (-0.2 5.56)
## 382 Addis Abeba Ethiopia 2823167 ETH POINT (38.74 9.03)
## 996 Algiers Algeria 2029936 DZA POINT (3.04 36.77)
## 1584 Antananarivo Madagascar 1463754 MDG POINT (47.51 -18.89)
## 2193 Asmara Eritrea 578860 ERI POINT (38.94 15.33)The capitals all have one latitude and one longitude value. The geometry of the point data is stored as POINT (Latitude, Longitude). On the location where the latitude and longitude overlap, a point will be drawn when POINT data is visualised. There is also another column that contains the population of the capital.
Let’s now visualise the African capitals by plotting their geometry using the tmap package.
tm_shape(africapitals) + #specify the data file
tm_dots() # displaying the point geometryThe tmap package works similar to the ggplot package. You need to first specify the data file you want to visualise using tm_shape(), after which the exact format of the spatial data can be specified (points, lines, polygons). As we are working with point data in this example, the tm_dots() function is used. As with ggplot, there is a lot of flexibility in the colouring, shapes and sizes of the dots. For example, the dots can be turned red and labelled with the name of the city.
tm_shape(africapitals) +
tm_dots("red")+ # displaying the point geometry as red dots
tm_text("capitalname", size=0.7 ) #adding the nameAs you can see in the example above, the labelling makes the image messy. In these instances it is important to think about the message you are trying to convey with your map. If the labelling is essential, you can look up the help section of the ‘tm_text’ using the help tool and play around with the different options to clean up the map further.
Exercise 1: In this first exercise, we will use the same African capital data as our example. Below, we have visualised all capitals with > 1.400.000 people using green squares of size 1. However, the code is not working. Can you find the four mistakes?
Hint: if you get stuck, look at ‘?tm_dots’
africapitals_filtered=africapitals %>%
dplyr::filter((africapitals$iso3c) > 1400000)
tm_shape(africapitals_filtered) +
tm_dots("green", size=0.5)Exercise 2: We will now use capital and African airport data.Visualise the capitals and airports in one map, with capitals as grey large filled-in circles and airports as smaller blue not-filled triangles.
Hint: if you get stuck, look at ‘Add Points to a Plot’ in the help section.
Hint: When both points and lines are mapped, datasets need to be identified seperately in tm_shape() before the use of tm_dots().
3.3 Lines
In previous episode we looked at point data, such as capitals and airports. We are often interested in how these different locations on a map are connected to each other. These connections are visualised using lines. Roads, rivers and flight paths are just a few of the many ways that lines are used. Lines are one dimensional data which are drawn using points (and thus point data) connected to each other in a set order. Depending on the detail of the lines, more or less point data are connected.
3.3.1 Example
For this example, we will look at the trans-African highway network. Let’s start by looking at a quick summary of the spatial aspects (geometry).
print(st_geometry(afrihighway)) #printing information on the geometry## Geometry set for 100 features
## Geometry type: LINESTRING
## Dimension: XYZ
## Bounding box: xmin: -17.38929 ymin: -33.95247 xmax: 43.13781 ymax: 37.08586
## z_range: zmin: 0 zmax: 0
## Geodetic CRS: WGS 84
## First 5 geometries:The results show that the African highway network contains 100 lines with geometry type LINESTRING.
Let’s now print the first 6 rows of data to see how line data are stored.
head(afrihighway) #First 6 rows of data are printed## Simple feature collection with 6 features and 1 field
## Geometry type: LINESTRING
## Dimension: XYZ
## Bounding box: xmin: -17.36938 ymin: 14.76957 xmax: -6.800537 ymax: 33.98436
## z_range: zmin: 0 zmax: 0
## Geodetic CRS: WGS 84
## # A tibble: 6 x 2
## Name geometry
## <chr> <LINESTRING [°]>
## 1 Western Sahara (Morocco… Z (-16.94778 21.34438 0, -16.85303 21.96343 0, -16.5…
## 2 Mauritania Border- Daka… Z (-17.36938 14.76957 0, -16.9519 14.77488 0, -16.73…
## 3 Nouakchott- Senegal Bor… Z (-15.81069 16.52036 0, -16.11694 16.72039 0, -16.1…
## 4 Western Sahara Border- … Z (-15.99128 18.08646 0, -16.01807 18.49003 0, -16.1…
## 5 Marrakesh- Western Saha… Z (-12.95837 27.67623 0, -12.7002 28.0041 0, -12.128…
## 6 Rabat- Marrakesh Link Z (-8.12439 31.79238 0, -8.02002 31.8589 0, -7.91564…Line data contain a string of data points with latitude and longitude: LINESTRING(Latitude1, Longitude1, Latitude2, Longitude2, Latitude3, Longitude3,.. ). During mapping, these points are connected to form a line.
Let’s visualise these linestrings in red by plotting their geometry using the tmap package.
tm_shape(afrihighway) +
tm_lines("red") Similar to point data, the lines can be illustrated in a large variety of ways. Please check the tm_lines() help section to familiarise yourself with the many layout options available.
Now we add the capitals from previous episode in blue.
tm_shape(africapitals) +
tm_dots("blue", size=0.5)+
tm_shape(afrihighway) +
tm_lines("red") It is great to see how the capitals are connected by the trans-African highway network.
Note The order of tm_dots() and tm_lines() matters. If you want the points overlaying the lines, it should be placed after the lines coding and visa versa.
Exercise 3: In the below exercise we have tried to visualise all the capitals and only the roads starting with the letter ‘b’. However, we have messed up the order of the code. Can you rearrange the code?
afrihighway_ex1=afrihighway[grep("^B", afrihighway$Name),]
tm_shape(africapitals) +
tm_dots("blue", size=0.5)+
tm_shape(afrihighway_ex1)+
tm_lines("blue")Exercise 4: Visualise the trans-African highway network, with line width associated with the length of the road. The function st_length is used to calculate the length of a line.
3.4 Polygons
Polygons are lines with the same first and last coordinate. When the polygon line is connected, the same start and end point results in a closed shape. Similar to lines, depending on the detail of the map, more or less points can be used to create a polygon. This two-dimensional data is most often used to visualise country and continent boundaries.
The continent outline of Africa is a multipolygon.
plot(st_geometry(africontinent), col = "lightblue")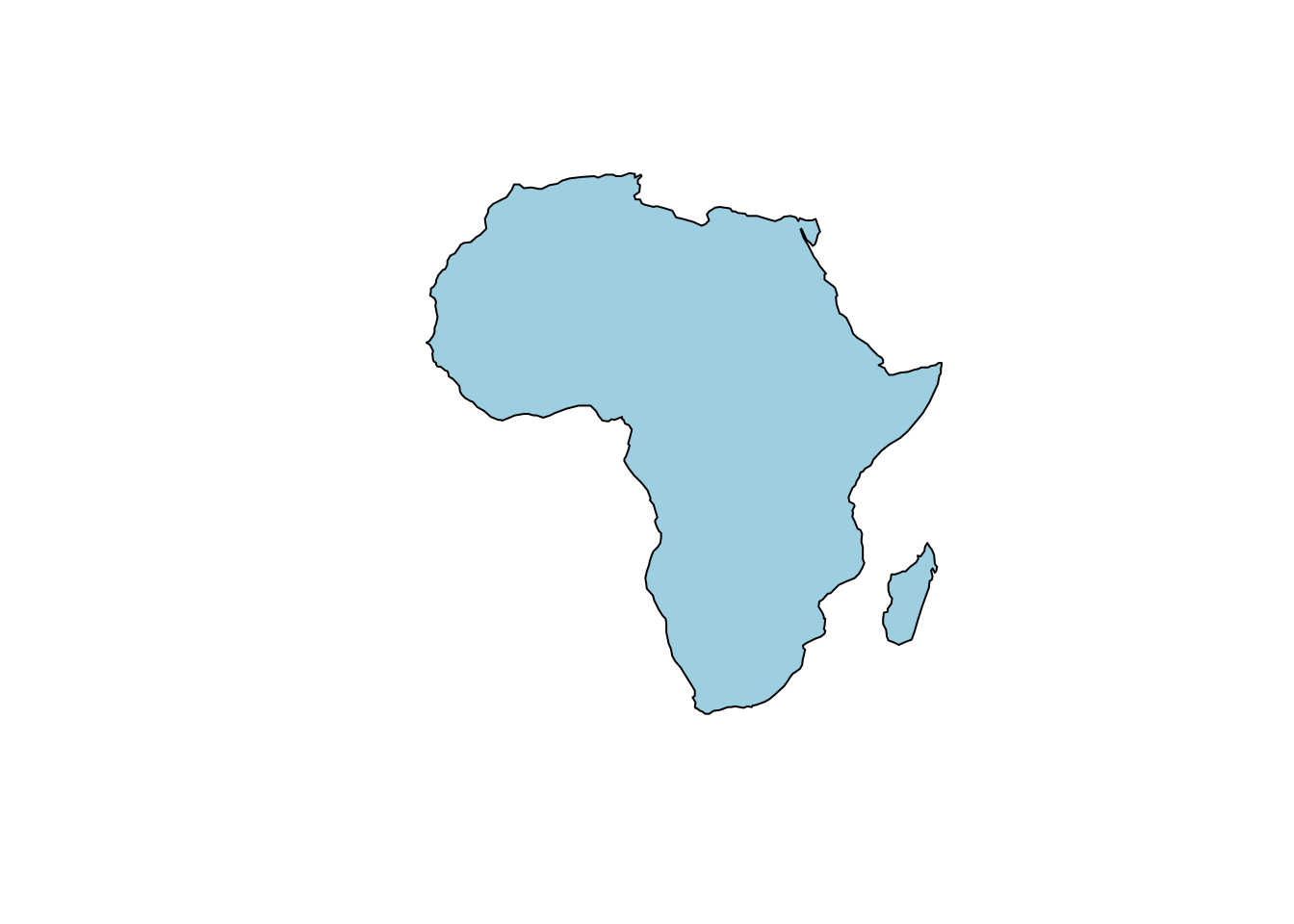
Figure 3.1: An outline map of Africa.
One polygon is used to visualise the mainland of Africa. An additional polygon is used for Madagascar. Together they represent the whole African continent.
Sometimes several polygons are necessary to capture a more complex shape. The different polygons in one data row indicate either areas to include or exclude from the final image. These are called multipolygons. An example of a multipolygon is the country border of South Africa. Lesotho is entirely surrounded by South Africa. If we want to visualise South Africa, we need to make sure that the Lesotho area is excluded. Visualisation of South Africa therefore requires two polygons, one to outline the outer borders and one to highlight the area to exclude (Lesotho country borders). Below, the South African border is visualised.
africountries_ex=africountries %>%
filter(`name` == "South Africa")
plot(st_geometry(africountries_ex), col = "lightblue")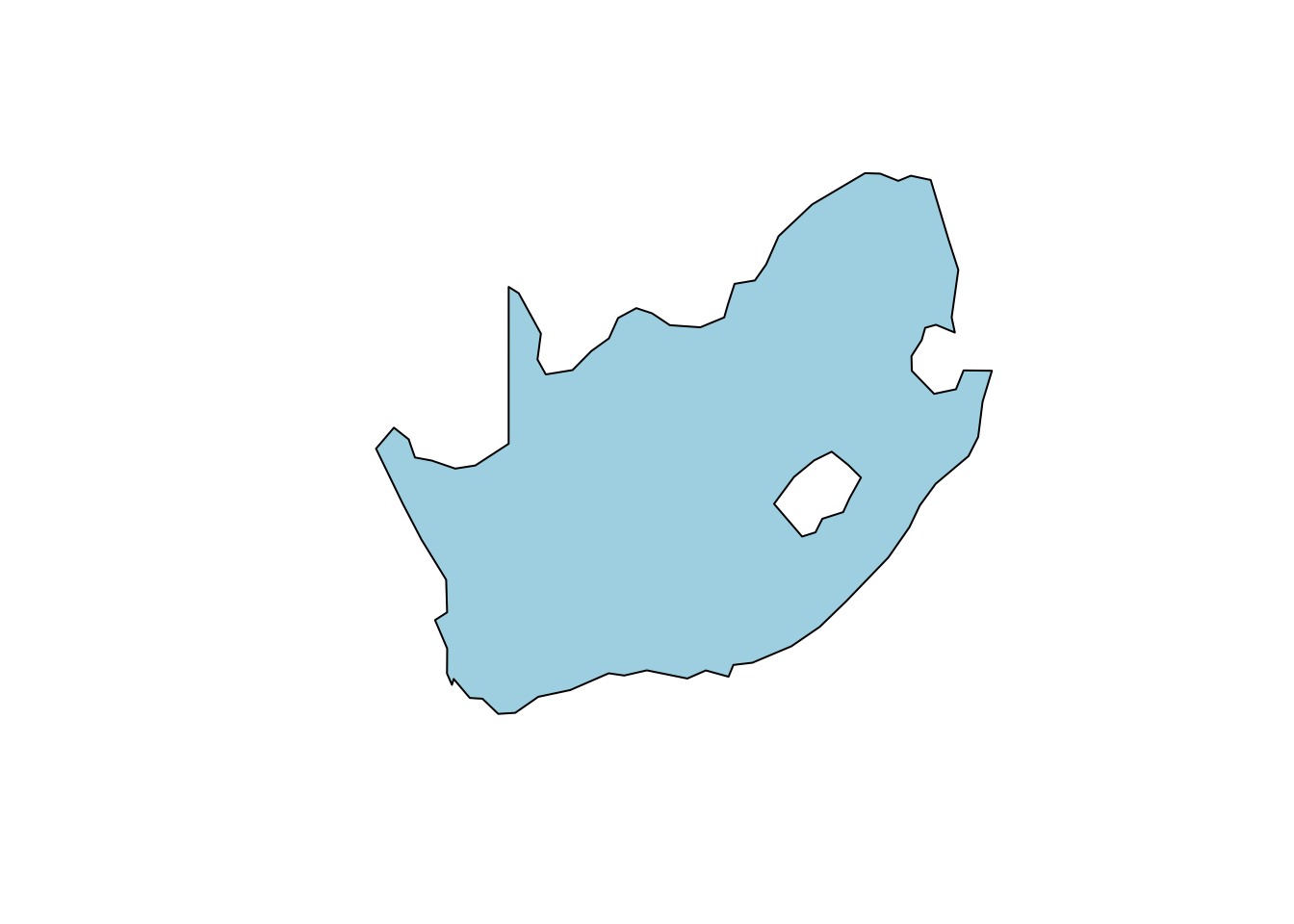
Figure 3.2: An outline map of South Africa.
As you can see in the image, when the polygon of South Africa is visualised, a white area is visible inside the country (representing Lesotho), which is not part of South Africa.
3.4.1 Example
For this example, we will look at the country borders of African countries. Let’s visualise the geometry of the datafile first.
print(st_geometry(africountries)) #printing information on the geometry## Geometry set for 51 features
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -17.62504 ymin: -34.81917 xmax: 51.13387 ymax: 37.34999
## Geodetic CRS: WGS 84
## First 5 geometries:The country border file contains 51 country outlines with geometry type MULTIPOLYGON.
If we print the first 6 rows of data, we can see how each country border is stored in the database.
head(africountries) #First 6 rows of data are printed## Simple feature collection with 6 features and 11 fields
## Geometry type: MULTIPOLYGON
## Dimension: XY
## Bounding box: xmin: -5.470565 ymin: -26.82854 xmax: 30.75226 ymax: 15.11616
## Geodetic CRS: WGS 84
## name name_long pop_est gdp_md_est lastcensus
## 1 Angola Angola 12799293 110300 1970
## 11 Burundi Burundi 8988091 3102 2008
## 13 Benin Benin 8791832 12830 2002
## 14 Burkina Faso Burkina Faso 15746232 17820 2006
## 25 Botswana Botswana 1990876 27060 2011
## 26 Central African Rep. Central African Republic 4511488 3198 2003
## income_grp iso_a3 geometry
## 1 3. Upper middle income AGO MULTIPOLYGON (((16.32653 -5...
## 11 5. Low income BDI MULTIPOLYGON (((29.34 -4.49...
## 13 5. Low income BEN MULTIPOLYGON (((2.691702 6....
## 14 5. Low income BFA MULTIPOLYGON (((-2.827496 9...
## 25 3. Upper middle income BWA MULTIPOLYGON (((25.64916 -1...
## 26 5. Low income CAF MULTIPOLYGON (((15.27946 7....
## name_fr name_pt
## 1 Angola Angola
## 11 Burundi Burundi
## 13 Bénin Benin
## 14 Burkina Faso Burquina Faso
## 25 Botswana Botsuana
## 26 République centrafricaine República Centro-Africana
## name_af name_sw
## 1 Angola Angola
## 11 Burundi Burundi
## 13 Benin Benin
## 14 Burkina Faso Bukinafaso
## 25 Botswana Botswana
## 26 Sentraal-Afrikaanse Republiek Jamhuri ya Afrika ya KatiHere, the geometry data contain a list with (multiple) polygons, with each polygon represented as a list of data points with latitude and longitude. These points are connected to form polygons, which are either used to include or exclude areas from the final image. The geometry of the multipolygon data is stored as MULTIPOLYGON (((Latitude1, Longitude1, Latitude2, Longitude2, Latitude3, Longitude3,.. ),(Latitude1, Longitude1, ..)),(Latitude1, Longitude1, …))).
Lets visualise these multipolygons with black lines.
tm_shape(africountries) +
tm_borders() #if only borders need to be visualisedtm_shape(africountries) +
tm_polygons() #if you want the image to specify the multipolygon areaNow we can add the capitals and highways from earlier :
tm_shape(africountries) +
tm_borders()+
tm_shape(africapitals) +
tm_dots("blue", size=0.5)+
tm_shape(afrihighway) +
tm_lines("red") Exercise 5: Multiple choice to identify if data files contain point, line or (multi)polygon geometry.
- Look up the bus routes in your home area. Which data type would you use to visualise this data?
- Point data
- Line data
- Multipolygon data
- All of the above
- What kind of data type is necessary to visualise the countries part of the the Economic Community of West African States (ECWAS) community?
- Point data
- Line data
- Multipolygon data
- All of the above
- Which data type is necessary for the authors to visualise the below image. (need help visualising this with the right approval from authors) https://www.google.com/url?sa=i&url=https%3A%2F%2Fcdiac.ess-dive.lbl.gov%2Fepubs%2Fndp%2Fndp055%2Fndp055.html&psig=AOvVaw2qJ0HAjtU9ytbSWT-qFR0R&ust=1616679119758000&source=images&cd=vfe&ved=0CAIQjRxqFwoTCKD8l5qFye8CFQAAAAAdAAAAABBW
- Point data
- Line data
- Multipolygon data
- All of the above
Exercise 6: Visualise the African borders of all countries with an area larger than 300.000 km^2. The function st_area is used to calculate the area within a polygon.
Hint: make sure you check the units
3.5 Rasters
Points, lines and polygons, in their essence, consist of points with a longitude and latitude value. The data files of these vectors look very similar. Raster data are a group on their own. Raster data consist of a matrix of grid cells (pixels), with each grid cell representing a geographical location with a value illustrating a characteristic of that location. Raster data are mainly used when displaying data that are continuous across space. For example, population density, landcover variation and elevation data extracted from satellites, drones and surveys.
The more grid cells a raster file contains, the smoother the visualisation of the characteristic will be. However, a large number of grids also means a large heavy file, which may be difficult to run. Whenever you are working with raster files, think about your goal and objective. The highest resolution might not always be necessary.
To read in raster data, we first need to install and load the ‘raster’ package.
#install.packages("raster") #install raster package
library(raster) # load raster packageWe can now start visualising raster data.
3.5.1 Example
For this example we use African population data from 2000 and 2020. Let’s look at the information within the file first.
print(afripop2000) #printing information on the raster data file## class : RasterLayer
## dimensions : 434, 413, 179242 (nrow, ncol, ncell)
## resolution : 0.1666667, 0.1666667 (x, y)
## extent : -17.62625, 51.20708, -34.97542, 37.35792 (xmin, xmax, ymin, ymax)
## crs : +proj=longlat +datum=WGS84 +no_defs
## source : memory
## names : ppp_2000_1km_Aggregated
## values : 0, 16606.66 (min, max)The population raster data from 2000 contains 434 rows, 413 columns and a total of 179242 grid cells with geometry type RasterLayer .
Let’s print the first 10 rows of data.
head(afripop2000) #First 6 rows of data are printed## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
## 1 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 2 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 3 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 4 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 5 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 6 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 7 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 8 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 9 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 10 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
## 20
## 1 NaN
## 2 NaN
## 3 NaN
## 4 NaN
## 5 NaN
## 6 NaN
## 7 NaN
## 8 NaN
## 9 NaN
## 10 NaNWhy do you think all rows are empty?
You could use getValues() to look at all grid cell values, but that would take up a few pages of the book, so we won’t do it here!
getValues(afripop2000)The printed matrix shows that the raster layer consists of a matrix with values. The grid cells can be empty if no data is available. This just results in no visualisation (NA or empty) at those locations.
Lets visualise the population data with the country borders. Note that population density data are highly skewed. To ensure both high and low density areas are clearly visible, we have to specify the data breaks manually.
tm_shape(afripop2020) +
tm_raster(breaks=c(0,2,20,200,2000,25000))We can make the image easier to interpret by using a palette from the viridisLite package, moving the legend using tm_layout() and including the African borders.
tm_shape(afripop2020) +
tm_raster(palette = rev(viridisLite::magma(5)), breaks=c(0,2,20,200,2000,25000)) + #specify the breaks of the palette
tm_layout(legend.position = c("left","bottom"))+ #moves the legend to the left bottom corner
tm_shape(africountries) +
tm_borders() Now we can add the capitals and highways from earlier :
tm_shape(afripop2000) +
tm_raster(palette = rev(viridisLite::magma(5)), breaks=c(0,2,20,200,2000,25000)) +
tm_layout(legend.position = c("left","bottom"))+
tm_shape(africountries) +
tm_borders() Exercise 7: Visualise the population data of 2000 using a different palette from the viridisLite package. Increase the number of breaks to six. Which breaks are most appropriate?
3.6 Further resources
If you are interested in learning more about the different spatial data types, please visit:
3.7 Summary
The image below gives a short recap of the different data types discussed in this chapter. You should now be able to recognize, load and manipulate these data types using the sf and raster and visualise them using the tmap package.
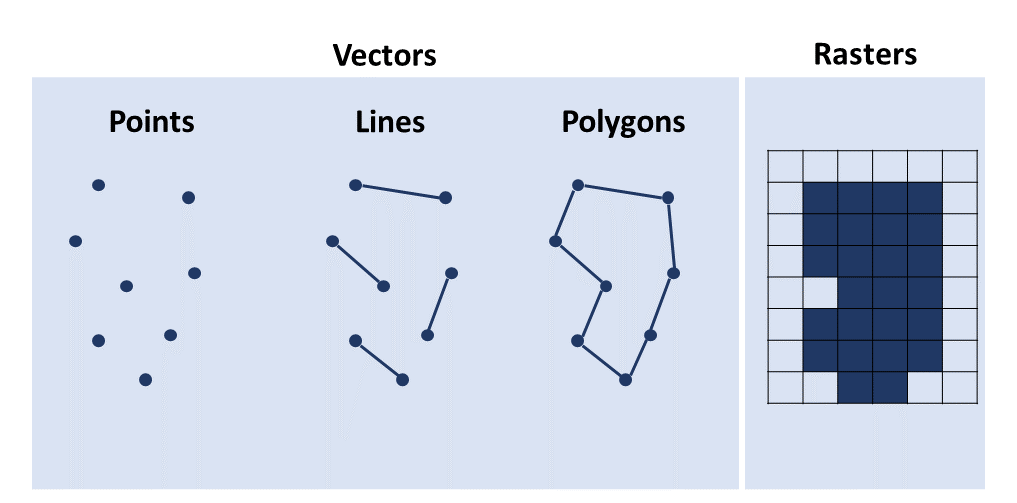
Figure 3.3: Summary of the chapter.
3.8 Exercise solutions
- Exercise 1
- In the initial filter,
africapitals$iso3cneeds to be changed toafricapitals$pop - Dots in 1.400.000 need to be removed
- The shape of the dots need to be specified as squares using
shape=22 - The size of the points needs to be 1.
- In the initial filter,
africapitals_filtered=africapitals %>%
dplyr::filter((africapitals$pop) > 1400000)
tm_shape(africapitals_filtered) +
tm_dots("green", shape = 22, size=1)- Exercise 2
tm_shape(africapitals) +
tm_dots(col="grey", shape = 19, size=3) +
tm_shape(afriairports) +
tm_dots(col="blue", shape = 2, size=1)- Exercise 3
afrihighway_ex1=afrihighway[grep("^B", afrihighway$Name),]
tm_shape(africapitals) + #important that capitals are visualised first
tm_dots("blue", size=0.5)+
tm_shape(afrihighway_ex1)+
tm_lines("blue")- Exercise 4
afrihighway$length=tapply(st_length(afrihighway), afrihighway$Name)
tm_shape(afrihighway) +
tm_lines(lwd = "length")- Exercise 5
- b
- c
- d
- Exercise 6
africountries$area_sqm <- st_area(africountries)
africountries$area_sqkm <-africountries$area_sqm / 1000000
africountries_filtered = africountries %>%
dplyr::filter(as.numeric(africountries$area_sqkm) > 300000)
tm_shape(africountries_filtered) +
tm_borders()- Exercise 7
tm_shape(afripop2020) +
tm_raster(palette = rev(viridisLite::plasma(6)), breaks=c(0,2,20,200,2000,20000, 25000)) +
tm_layout(legend.position = c("left","bottom"))+
tm_shape(africountries) +
tm_borders()